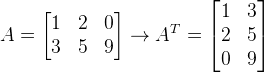一、矩阵和向量
1、矩阵
矩阵一般用大写字母表示
(1)矩阵示例:
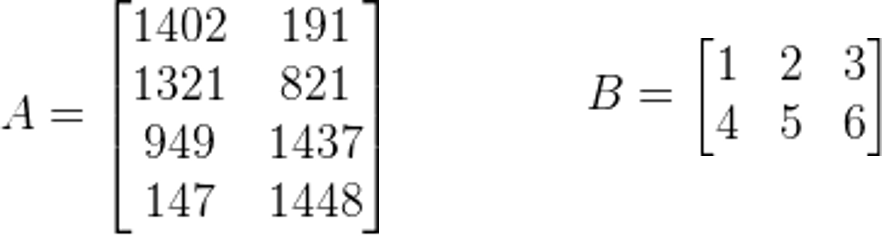
(2)矩阵维度:矩阵的行数*矩阵的列数
在上图矩阵中,A的维度是4*2=8,B的维度是2*3=6
(3)![]() 表示矩阵A的第i行第j列的元素。
表示矩阵A的第i行第j列的元素。
以矩阵A为例: ![]() = 1402
= 1402 ![]() = 191
= 191 ![]() = 1437
= 1437 ![]() = Undefined(Error)
= Undefined(Error)
(4)矩阵记法,记作![]() ,其中m表示矩阵的行数,n表示矩阵的列数。
,其中m表示矩阵的行数,n表示矩阵的列数。
上述A矩阵可表示为:![]() ,上述B矩阵可表示为:
,上述B矩阵可表示为:![]()
2、向量
向量一般用小写字母表示
(1)向量就是维数为n*1的矩阵。
(2)向量示例:
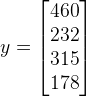
此向量是一个四维向量,含有四个元素,用![]() 表示。
表示。
(3)用![]() 表示向量的第i个元素。
表示向量的第i个元素。 ![]() = 460
= 460 ![]() = 315
= 315
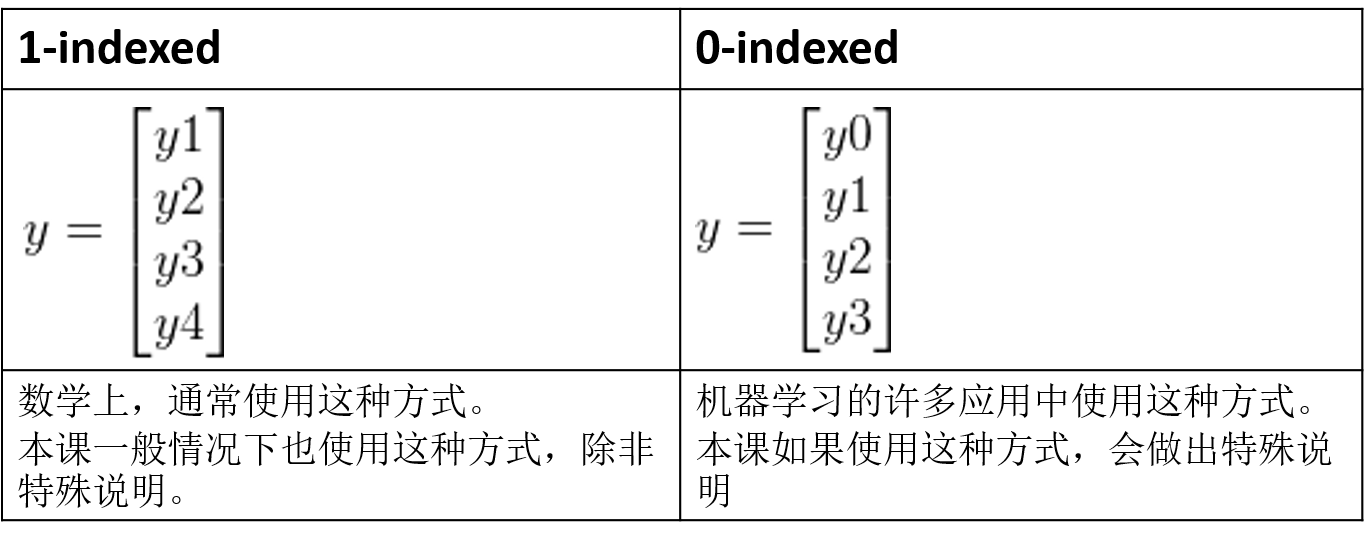
(4)1-indexed VS 0-indexed
二、加法和标量乘法
1、矩阵加法(要求两矩阵同维)
示例: 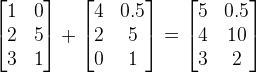
2、标量乘法
所谓标量,是指一个实数,标量乘法即实数和矩阵相乘。
示例:
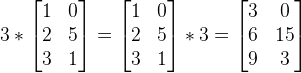
![]()
(3)结合算法示例: 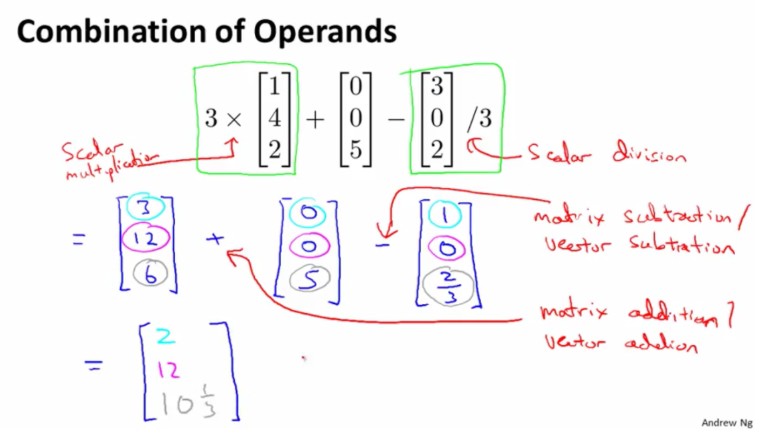
三、矩阵向量相乘
1、矩阵向量乘法的细节如下图: 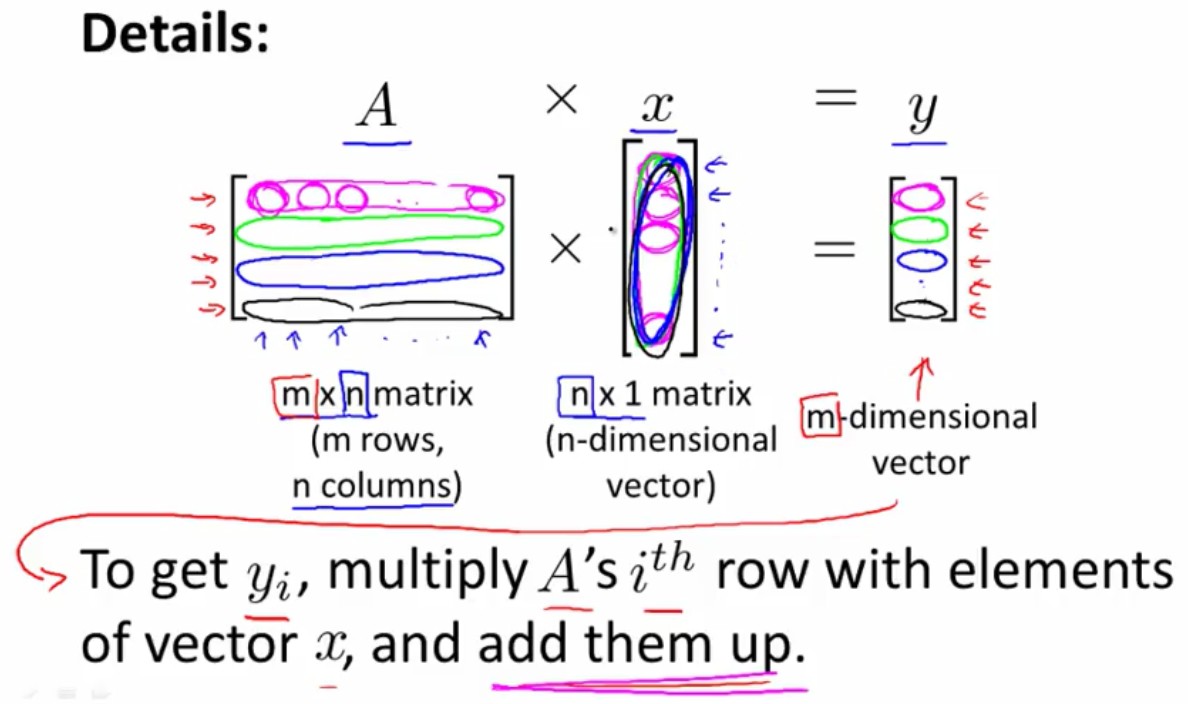
2、示例:
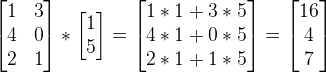
3、将矩阵向量相乘运用到机器学习中: 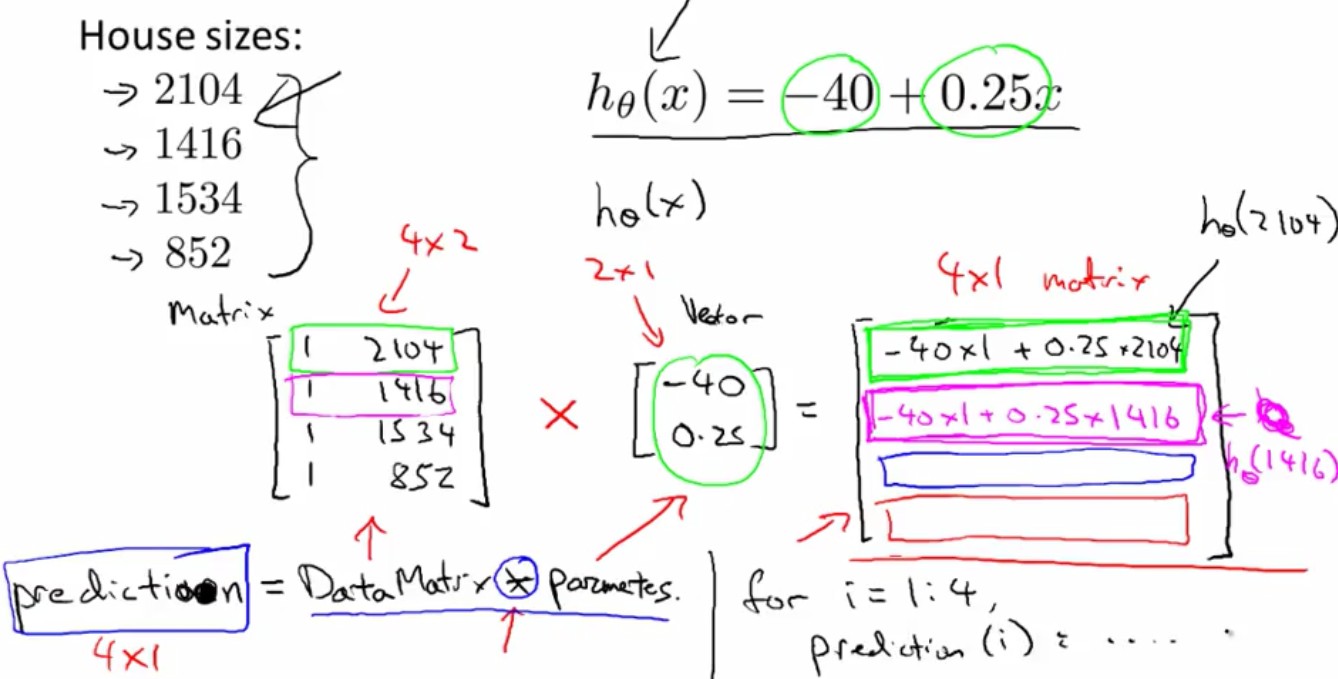
有四间房子的大小分别为:2104,1416,1534,852。其拟合函数h(x)=-40+0.25*x;
则算出这四间房子对应的h(x)的大小,可以采用下面的方法: 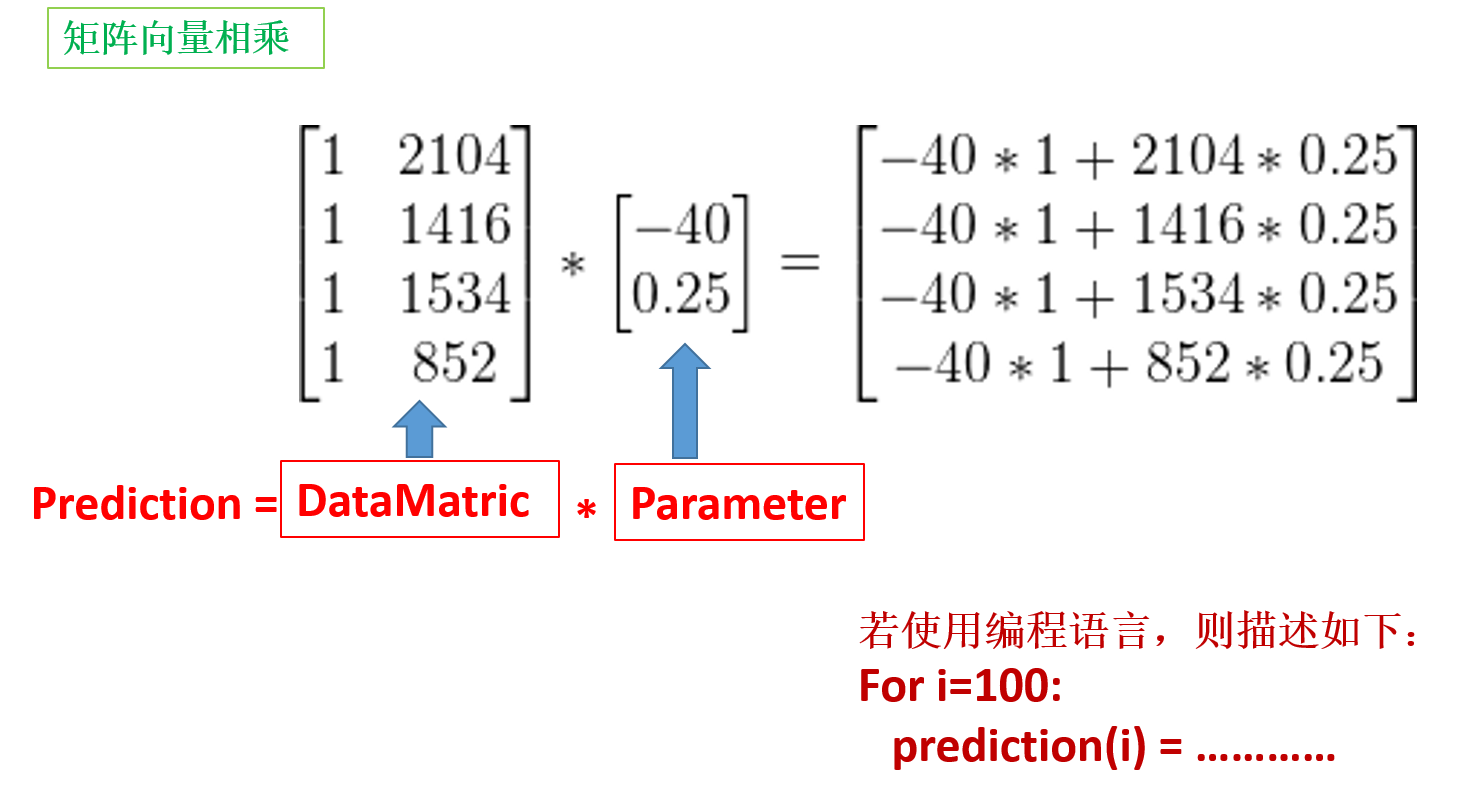
四、矩阵和矩阵相乘
1、矩阵与矩阵相乘的细节部分: 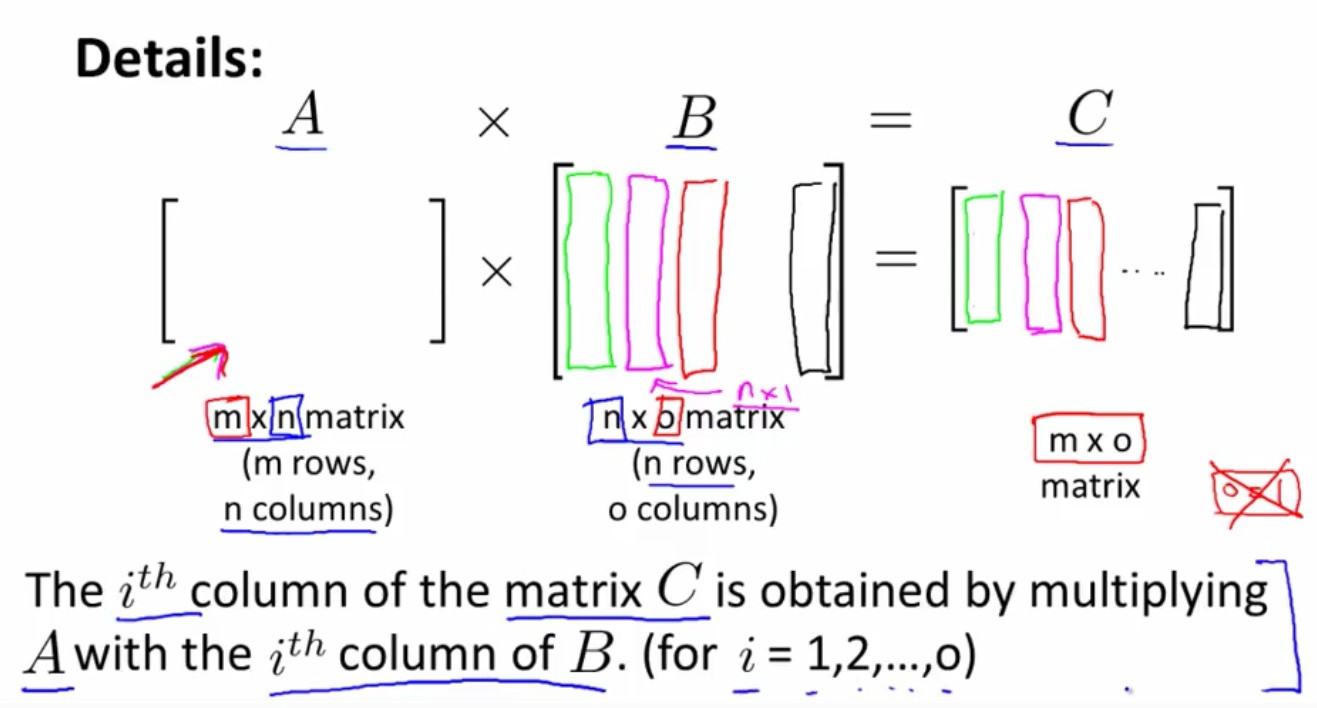
2、矩阵与矩阵相乘的示例:

3、矩阵与矩阵乘法的应用 
五、矩阵乘法的性质
1、不满足交换律,即A*B≠B*A
2、满足结合律,即A*B*C=(A*B)C=A(B*C)
3、数乘运算
单位阵:对角线元素为1,其他位置元素为0,例如,![]() 和
和 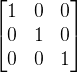 。
。

六、逆矩阵和转置矩阵
1、逆矩阵
若A是m*m矩阵且A有逆矩阵,则![]() (I为单位阵)
(I为单位阵)
注:
(1)只有方阵存在逆矩阵。
(2)O矩阵不存在逆矩阵,因为找不到一个矩阵和O矩阵相乘得到单位阵。
(3)不存在逆矩阵的矩阵叫做奇异矩阵或者退化矩阵,例如O矩阵。
2、转置矩阵
令A是m*n矩阵,B=![]() ,则B是n*m矩阵,且
,则B是n*m矩阵,且![]()
举例: